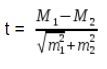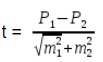Распределение признака в выборочной совокупности
Весь смысл выборочной совокупности в том, чтоб по ней можно было судить о генеральной совокупности, для этого выборка должна быть репрезентативной. Репрезентативность достигается в том числе достаточным количеством наблюдений (n).
Параметры распределения
Важнейшие параметры распределения случайной величины Х являются - математическое ожидание µ (Мген) и дисперсия σ2.
- Математическое ожидание (Х) - среднее значение случайной величины при стремлении количества выборок к бесконечности.
- Среднеквадратичное отклонение (σ2) - показатель рассеивания значений случайной величины относительно ей математического ожидания.
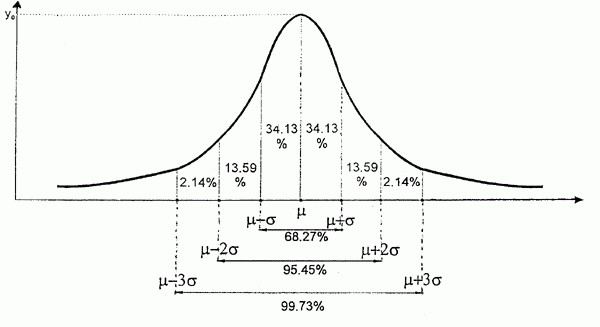
Распределения бывают непрерывными и дискретными. Наиболее известно из непрерывних распределений - нормальное.
Характеристики нормального распределения
- Совпадение средней арифметической (М), медианы (Ме) и моды (Мо).
- Чем больше величина отклоняется от среднего значения, тем меньше частота его встречаемости.
Первичные величины, характеризующие распределение
- Средняя арифметическая (М)
- Среднее квадратичное отклонение (σ2)
- Коэффициент вариации
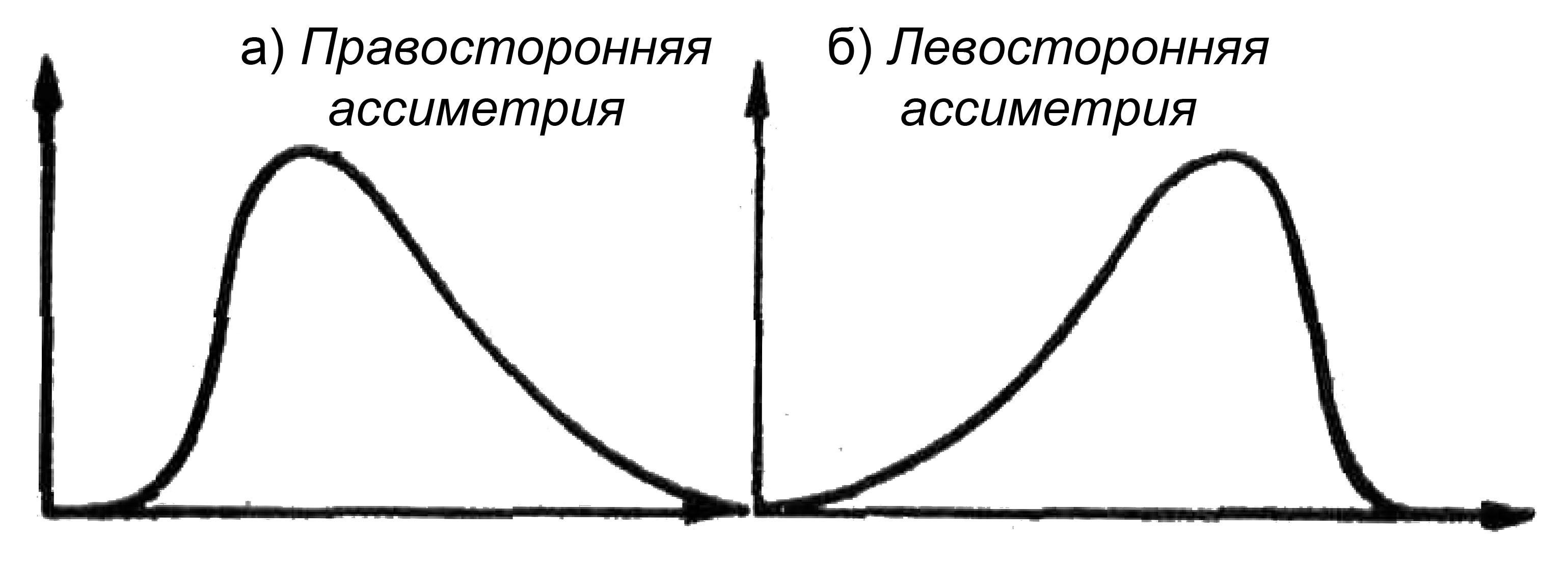
- Коэффициент асимметрии - показатель отклонения распределения в левую и правую сторону по оси абсцесс. Если больше влево - левосторонняя или отрицательная. Если вправо - правосторонняя положительная.
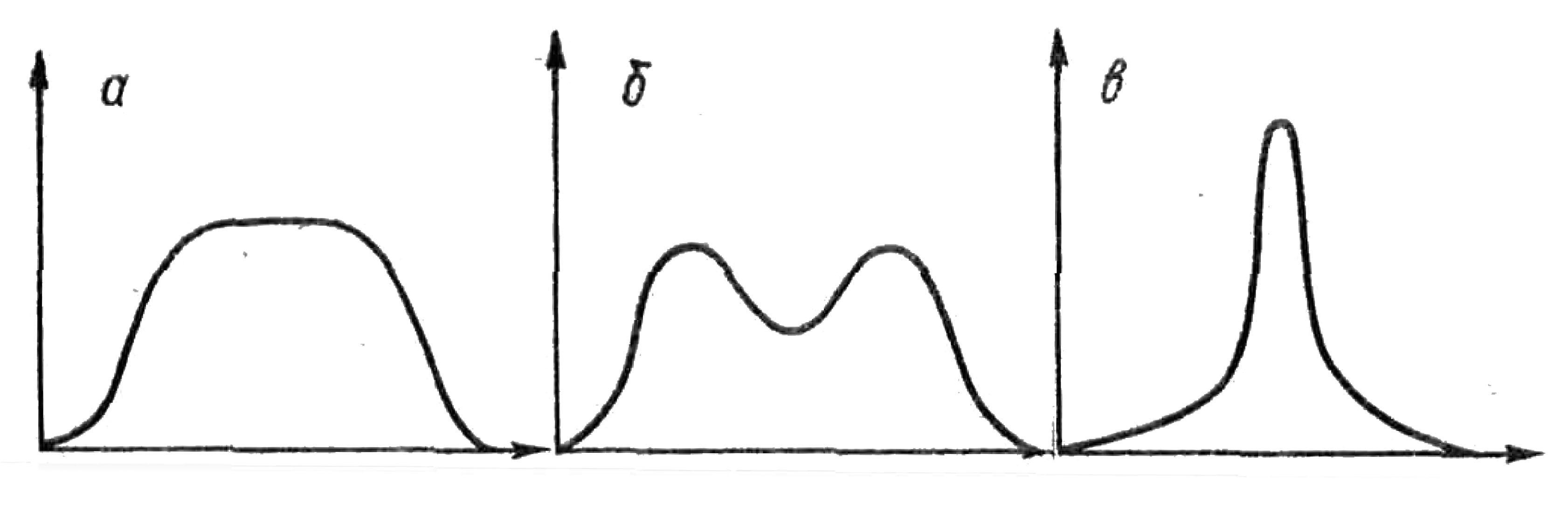
- Эксцесс - мера сглаженности. Если близко к 0, то форма распределения близка к нормальному виду. Если > 0 - то форма остроконечная. Если < 0 - форма плосковершинная. Норма эксцесса от -1 до +1.
Значение нормального распределения
Если нормальное распределение, для обработки используют параметрические методы математической статистики для расчёта достоверности различий между выборками:
- Критерий Стьюдента (t)
- Критерий Фишера (F)
- Коэффициент корреляции Пирсона (r)
Если кривая распределения отлична от нормальной, используют методы непараметрической статистики, расчёт достоверности разности по
- Критерию Манна-Уитни (U)
- Коэффициенту ранговой корреляции Спирмена (p)
Альтернативное (дихотомическое) распределение
Параметр математического ожидания выражает относительную величину (долю) единиц совокупности, не которые обладают изученным признаком (Р). Доля совокупности, не обладающая признаком, обозначается q.
Как правило, q = 10 - P.
Дисперсия в таком случае: Рв = nx/nв
Ошибки репрезентативности
- Ошибка выборочного наблюдения (mвн) - разность между значением параметра в генеральной совокупности и его выборочным значением.
Для среднего значения mвн = | Мген - Мв |; для доли: mвн = | Рген - Рв |.
- Средняя ошибка (m) - величина, выражающая среднее квадратичное отклонение выборочной средней от математического ожидания:
m = √(σ2/n) - Соотношение дисперсий между выборочной и генеральной совокупностями:
σ2=σ2в × n/(n-1)
При достаточно больших выборках (n) можно считать, что σ2=σ2в
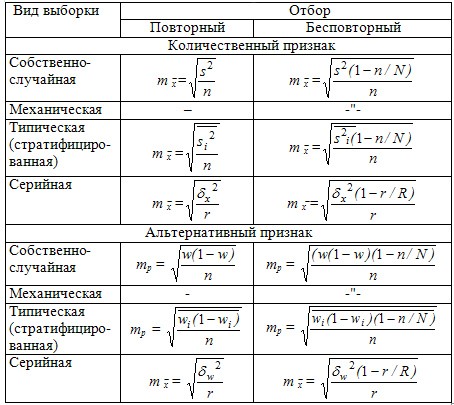
Расчёт средней ошибки (m) для разных видов выборок
На практике чаще используются следующие формулы
- Расчёт ошибки репрезентативности средней арифметической (mM):
mM=σ/√n - Расчёт ошибки репрезентативности относительной величины (mp):
mp=√(P*q / n)
где P - относительная величина (проценты, промилле и т.д.)
q - доля единиц совокупности с альтернативным признаком (1-Р или 100-Р или 1000-Р) в зависимости от основания, на которое рассчитан коэффициент
n - численность выборки
- Если в испытании объём выборки менее 30, то n уменьшается на 1:
(n-1)
Вероятность безошибочного прогноза
В медицинских исследований достаточная вероятность - 95-99%. В некоторых случаях должный прогноз - 99,7%.
Определённой вероятности безошибочного прогноза соответствует величина предельной ошибки случайной выборки (Δ).
Δ = t × m
где t - доверительный коэффициент (критерий Стьюдента)
m - средняя ошибка выборки
Вероятность прогноза (р) при значении критерия Стьюдента (t)
| t | p |
|---|---|
| < 1.96 | < 0.95 |
| 2 | 0.954 |
| 2.5 | 0.988 |
| 3 | 0.997 |
| 3.5 | 0.999 |
- Предельная ошибка выборки:
Δ = t × √( σ2 ÷ n) - Необходимая численность выборки:
n = t2 × σ2 ÷ Δ2
Для определения достоверности различий между двумя показателями или средними величинами при малом числе наблюдений (n ≤ 30, в каждой группе) критерий достоверности оценивается по таблице значений t-критерия Стьюдента по числу степеней свободы/ При этом число степеней свободы определяется, как n´= n1 + n2 - 2.
| Число степеней свободы, n´ | Значение t-критерия Стьюдента при p=0.05 |
|---|---|
| 1 | 12.706 |
| 2 | 4.303 |
| 3 | 3.182 |
| 4 | 2.776 |
| 5 | 2.571 |
| 6 | 2.447 |
| 7 | 2.365 |
| 8 | 2.306 |
| 9 | 2.262 |
| 10 | 2.228 |
| 11 | 2.201 |
| 12 | 2.179 |
| 13 | 2.160 |
| 14 | 2.145 |
| 15 | 2.131 |
| 16 | 2.120 |
| 17 | 2.110 |
| 18 | 2.101 |
| 19 | 2.093 |
| 20 | 2.086 |
| 21 | 2.080 |
| 22 | 2.074 |
| 23 | 2.069 |
| 24 | 2.064 |
| 25 | 2.060 |
| 26 | 2.056 |
| 27 | 2.052 |
| 28 | 2.048 |
| 29 | 2.045 |
| 30 | 2.042 |
| 31 | 2.040 |
| 32 | 2.037 |
| 33 | 2.035 |
| 34 | 2.032 |
| 35 | 2.030 |
| 36 | 2.028 |
| 37 | 2.026 |
| 38 | 2.024 |
| 40-41 | 2.021 |
| 42-43 | 2.018 |
| 44-45 | 2.015 |
| 46-47 | 2.013 |
| 48-49 | 2.011 |
| 50-51 | 2.009 |
| 52-53 | 2.007 |
| 54-55 | 2.005 |
| 56-57 | 2.003 |
| 58-59 | 2.002 |
| 60-61 | 2.000 |
| 62-63 | 1.999 |
| 64-65 | 1.998 |
| 66-67 | 1.997 |
| 68-69 | 1.995 |
| 70-71 | 1.994 |
| 72-73 | 1.993 |
| 74-75 | 1.993 |
| 76-77 | 1.992 |
| 78-79 | 1.991 |
| 80-89 | 1.990 |
| 90-99 | 1.987 |
| 100-119 | 1.984 |
| 120-139 | 1.980 |
| 140-159 | 1.977 |
| 160-179 | 1.975 |
| 180-199 | 1.973 |
| 200 | 1.972 |
| ∞ | 1.960 |
Оценка достоверности разности величин
где М1 и М2, Р1 и Р2 — статистические величины, полученные при проведении выборочных исследований;
m1 и m2; — их ошибки репрезентативности; t — коэффициент достоверности.