Корреляционный анализ
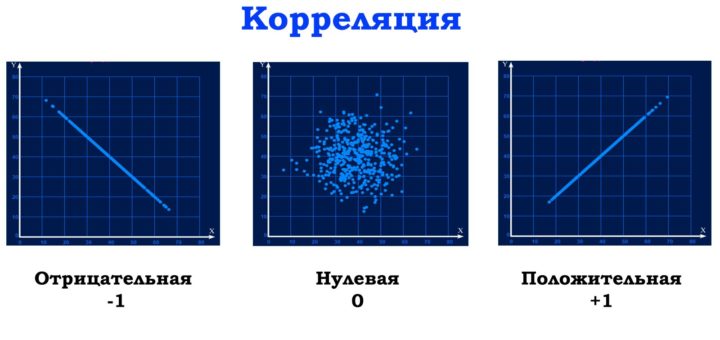
Корреляционный анализ позволяет найти зависимость среди нескольких случайных величин.
По форме корреляционной связи
- Прямолинейная корреляционная связь - равномерные изменения одного признака примерно соответствуют равномерным изменениям второго.
- Криволинейная связь - равномерные изменения одного признака, соответствуют неравномерным изменениям второго признака, причем неравномерность имеет определенную закономерность.
Виды связи между признаками
- Функциональная – изменение величины одного признака неизменно вызывает изменение другого признака. Например, зависимость площади круга от радиуса, расстояния от времени и скорости.
- Корреляционная – величине одного признака соответствует ряд варьирующих значений другого признака (зависимость роста ребенка от возраста, зависимость частоты пульса от температуры тела, зависимость частоты обострений хронических заболеваний от возраста, зависимость смертности от рака легких в зависимости от количества промышленных выбросов в атмосферный воздух и т.д.).
Направление линейной корреляции
В зависимости от коэффициента корреляции Пирсона (r):
- если r > 0, то связь прямая (положительная), т.е. при возрастании одной величины другая в среднем тоже возрастает;
- если r < 0, то связь обратная (отрицательная), т.е. при возрастании одной величины другая имеет тенденцию в среднем убывать.
- если статистическая связь между признаками отсутствует, то r = 0.
Глубина (сила) корреляции
- если
0 < | r | ≤ 0,3, то связь слабая; - если
0,3 < | r | ≤ 0,5, то связь умеренная; - если
0,5 < | r | ≤ 0,7, то связь значительная; - если
0,7 < | r | ≤ 0,9, то связь сильная; - если
0,9 < | r | ≤ 1, то связь очень сильная. - При
| r | = 1связь между величинами функциональная.
Формулы расчёта
- Коэффициент корреляции рядов (rxy) (Пирсона):
rxy = 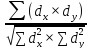
где d = V- M.
- средняя ошибка коэффициента корреляции:
- при числе наблюдений более 100;
mr = 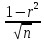
- при числе наблюдений от 30 до 100;
mr = 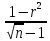
- при числе наблюдений менее 30.
mr = 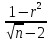
- при числе наблюдений более 100;
- Для оценки величины полученной ошибки следует использовать критерий достоверности (t).
t = 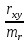
Непараметрические методы
Непараметрические методы не основываются на оценке параметров (таких как среднее или стандартное отклонение) при описании выборочного распределения интересующей величины. Поэтому эти методы иногда также называются свободными от параметров или свободно распределенными.
Непараметрические процедуры позволяют обрабатывать данные "низкого качества" из выборок малого объема с переменными, про распределение которых мало что или вообще ничего не известно. Непараметрические методы как раз и разработаны для тех ситуаций, достаточно часто возникающих на практике, когда исследователь ничего не знает о параметрах исследуемой популяции (отсюда и название методов - непараметрические).
Коэффициент корреляции рангов (р) (Спирмена)
Коэффициент корреляции рангов относится к непарамегрическим критериям. Он используется при необходимости получения быстрого результата, при малом числе наблюдений, а также в тех случаях, когда изучаемые признаки не имеют точных количественных значений или носят описательный характер. Этот метод основан на определении ранга (места) каждого из значений ряда.
| ρ = 1- |
где
d — разность между ранговыми номерами,
n — число парных членов в коррелируемых рядах.
Вычисления проводятся по следующему алгоритму:
- Определить ранги по значению каждой величины ряда. (1,2,3,4…) Если первый ряд (x) ранжируется от меньшего значения к большему, то второй ряд (у) следует ранжировать в том же порядке.
- Определить разность рангов каждой пары ряда (х) и ряда (у): (dxy)= (x) - (у). Они в сумме с учетом знаков равны нулю.
- Возвести в квадрат полученные разности и суммировать их.
- Рассчитать коэффициент корреляции рангов по формуле.
Прежде чем судить о степени связи между изучаемыми признаками, необходимо оценить достоверность коэффициента корреляции рангов.
| t = |
Полученное значение критерия t оценивается по таблице t-критерия Стьюдента для числа степеней свободы n' = n-2. Коэффициент корреляции незначим, если рассчитанное значение меньше табличного.